Machine Learning Algorithms
ML Algorithms with Python
- Difference between Supervised & Unsupervised Learning?
- How to pick which algorithm to use?
- How to set up algorithm and scale data?
- What is a Training & Testing set?
Algorithms in Machine Learning:
Supervised Learning
Let's say we are given a data set with points of type x(1),..., x(n). Then we are also given a data set or single column of known outputs y(1) ,..., y(n). Our goal is to create a model that will learn how to predict the outcomes of x, which are y.
Linear Models:
We assume here that y|x; θ ∼ N (μ,σ2). By noting X the matrix design, the value of θ that minimizes the cost function is a closed-form solution such that:
Least Means Square:
Locally Weighted Regression:
Logistic Regression:
Softmax Regression:
Exponential Models:
Most common exponential distributions summed up in the following table:
Support Vector Machines (SVM):
Gaussian Discriminant Analysis:
Naive Bayes:
The Naive Bayes model supposes that the features of each data point are all independent:
Maximizing the log-likelihood gives the following solutions, with k ∈ {0,1}, l ∈ [1,L]. This method is usually for text classification and spam detection.
Random Forrest:
K-nearest neighbors:
The k-nearest neighbors algorithm, commonly known as k-NN, is a non-parametric approach where the response of a data point is determined by the nature of its k neighbors from the training set. It can be used in both classification and regression settings.
Unsupervised Learning
Clustering:
Latent variables are hidden/unobserved variables that make estimation problems difficult, and are often denoted z. Here are the most common settings where there are latent variables:
k-means clustering:
After randomly initializing the cluster centroids μ1,μ2,...,μk ∈ Rn, the k-means algorithm repeats the following step until convergence:
We note c(i) the cluster of data point i and μj the center of cluster j.
Hierarchical clustering:
It is a clustering algorithm with an agglomerative hierarchical approach that build nested clusters in a successive manner. There are different sorts of hierarchical clustering algorithms that aims at optimizing different objective functions, which is summed up in the table below:
Calinski-Harabaz Index:
By noting k the number of clusters, Bk and Wk the between and within-clustering dispersion matrices respectively defined as:
The Calinski-Harabaz index s(k) indicates how well a clustering model defines its clusters, such that the higher the score, the more dense and well separated the clusters are. It is defined as follows:
Principle Component Analysis:
Given a matrix A ∈ Rn×n, λ is said to be an eigenvalue of A if there exists a vector z ∈ Rn\{0}, called eigenvector, such that we have:
Let A ∈ Rn×n. If A is symmetric, then A is diagonalizable by a real orthogonal matrix U ∈ Rn×n. By noting Λ = diag(λ1,...,λn), we have:
We assume that our data x has been generated by the n-dimensional source vector s = (s1,...,sn), where si are independent random variables, via a mixing and non-singular matrix A as follows:
The goal is to find the unmixing matrix W = A−1 by an update rule.
Probability / Likelihood / Stochastic Gradient
Important Statistics & Set-ups
Classification:
Regression:
The coefficient of determination, often noted R2 or r2, provides a measure of how well the observed outcomes are replicated by the model and is defined as follows:
Model Selection:
Cross-validation, also noted CV, is a method that is used to select a model that does not rely too much on the initial training set. The most commonly used method is called k-fold cross-validation and splits the training data into k folds to validate the model on one fold while training the model on the k − 1 other folds, all of this k times. The error is then averaged over the k folds and is named cross-validation error.
Interpretation:
The bias of a model is the difference between the expected prediction and the correct model that we try to predict for given data points. The variance of a model is the variability of the model prediction for given data points. The simpler the model, the higher the bias, and the more complex the model, the higher the variance.
In all this page was an introduction/summary to most of the methods and algorithms in supervised and unsupervised machine learning. This was meant to explain the more hardcore mathematical approach on how these algorithms work, and how to alter them when conducting and creating your own machine learning algorithms and perhaps when to use one.
Please see my GitHub page on the implementation of machine learning algorithms using datasets found on the web.
Thank you,
Jose Hernandez

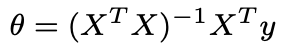




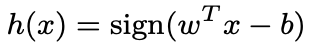







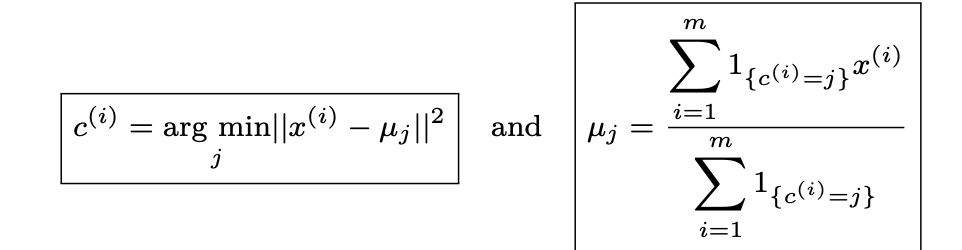





















Comments
Post a Comment